Conway's Game of Life

Life, devised by John Conway, is a zero-player game that, while simple, has roots in automata theory, evolution, chaos theory, AI, Gödel's incompleteness theorems, free will, etc.

The universe of Life is an infinite, 2D cellular automaton where each element (a square cell) is either dead or live (0 or 1). Every cell interacts with its eight neighbours. And at each tick, the following rules follow:

1. Any live cell with two or three live neighbours survives.
2. Any dead cell with three live neighbours becomes a live cell.
3. All other cells die or stay dead.

The Universe

Let's build this block by block.

Firstly, we need an infinite, two-dimensional orthogonal grid of square cells to contain our population. Unfortunately, my system can't simulate infinity, so ours will be a bounded m x n grid as you see here:

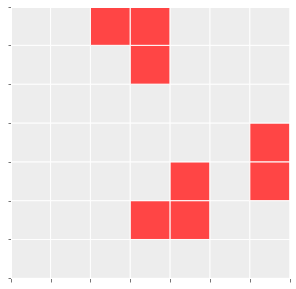
This is a random seed. A red cell indicates Live. Meanwhile, all other cells are Dead.

Genesis

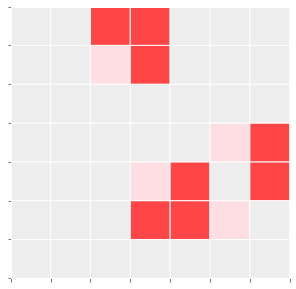
Any live cell with two or three live neighbours survives. Any dead cell with three live neighbours becomes a live cell.

If we simulate the next generation (iteration) basis the above rules, we can enumerate all the cells that will be Live in the next iteration (Interim Live):

Death

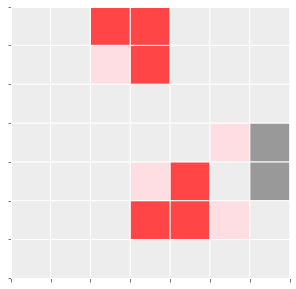
All other cells die or stay dead.

To complete the tick (phase iteration), we also need to assess all the cells that will be Dead by the next tick (Interim Dead):

The Cycle

Applying the above rules simultaneously, we get the following phase after one iteration:

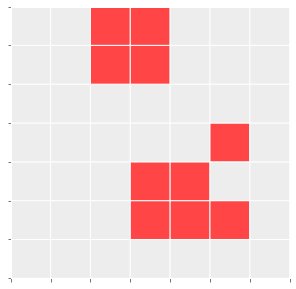
N Epochs

Estimating phase value after one tick was simple enough. But can you estimate the phase value after 10 epochs? What about 100? Does the system ever halt?

For our case, the system halts after 7 epochs (as all cells are Dead):

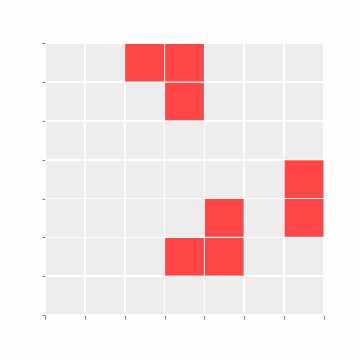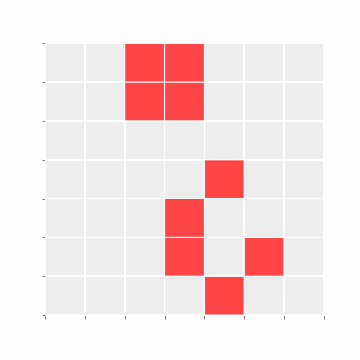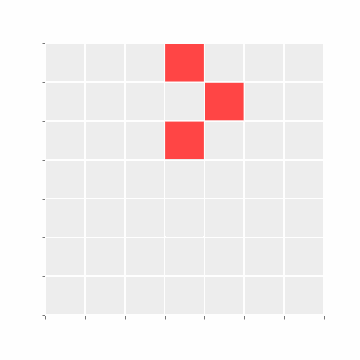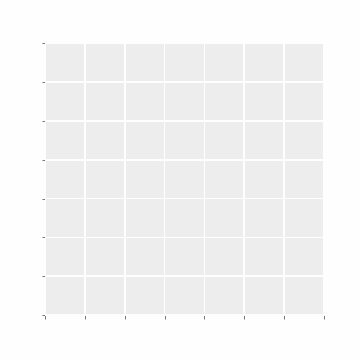
Undecidability

But ultimately, the Game of Life is undecidable — given an initial pattern and a later pattern, no algorithm can be devised to predict whether the latter is ever going to appear. Patterns in the GoL might come to a halt, get stuck in a loop, grow chaotic and proliferate (like microorganisms) — with or without an eventual convergence. As such, the GoL demonstrates how simplicity generates complexity, providing an analogy for all mathematics (& the universe).

Samples

I went through the trouble of simulating the experiment like 100 times. Some results were interesting, but eventually, I just scouted cool-looking seeds and tacked on their results (you're welcome!).

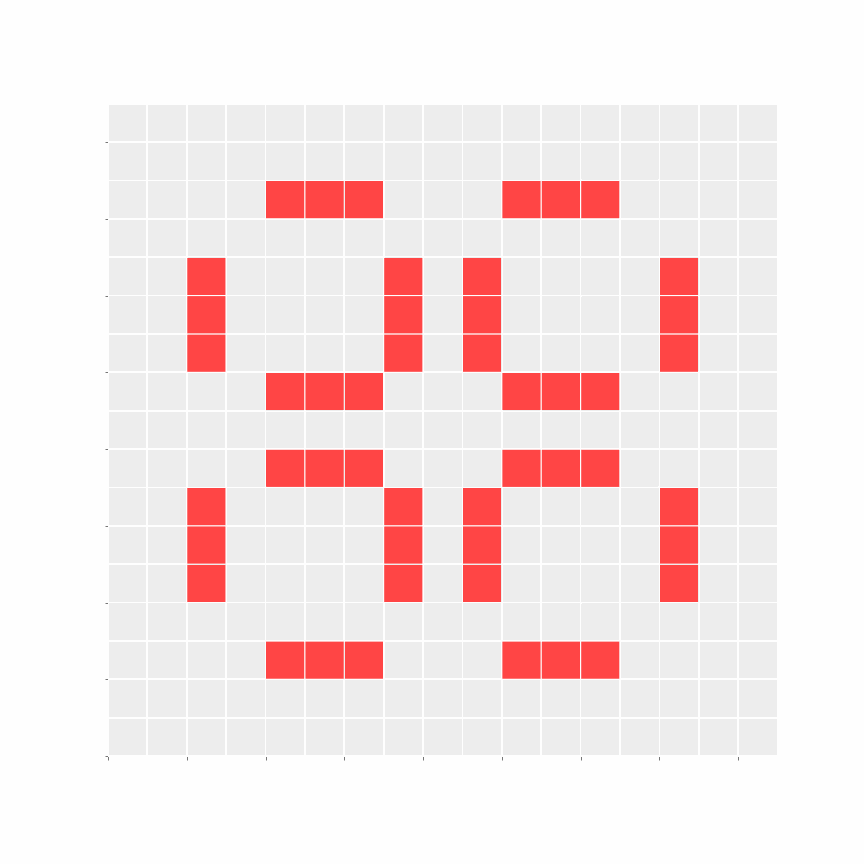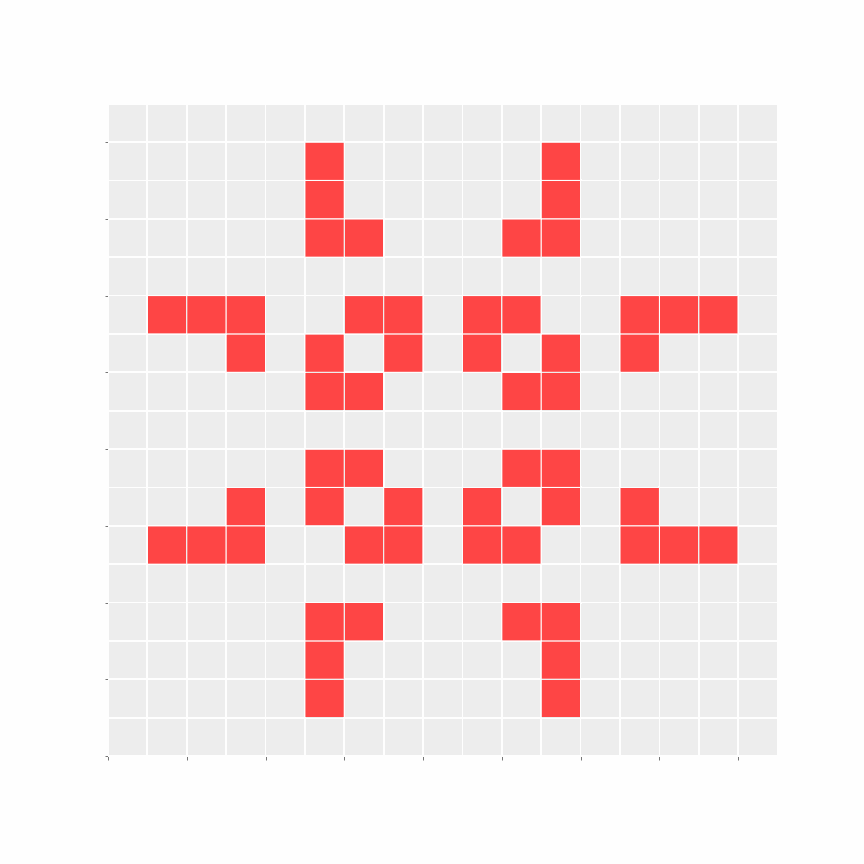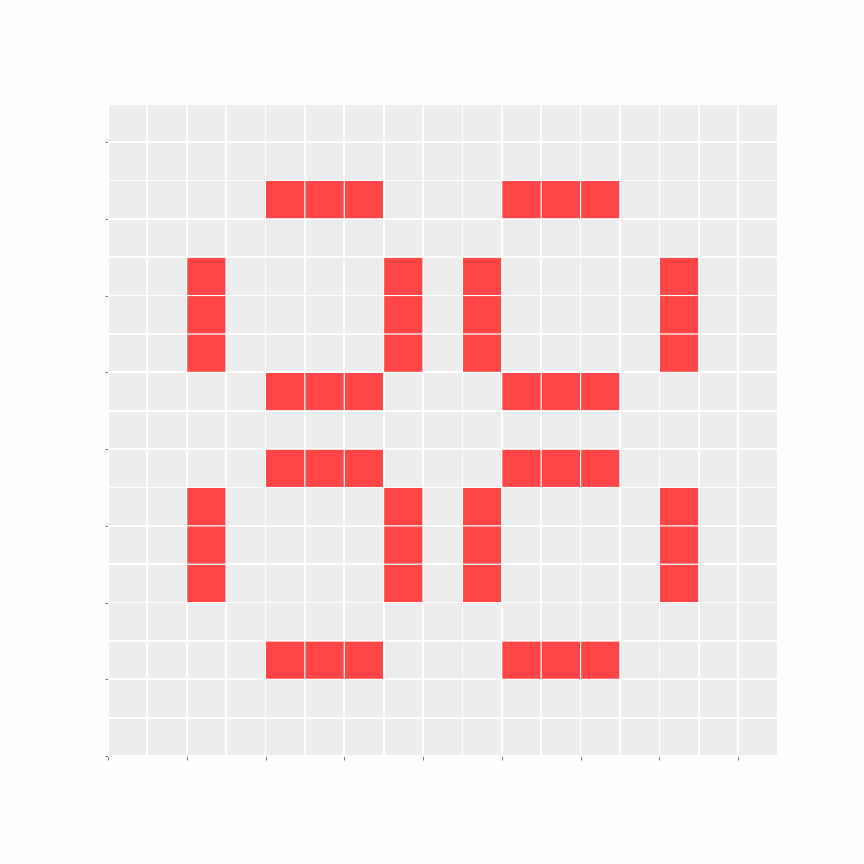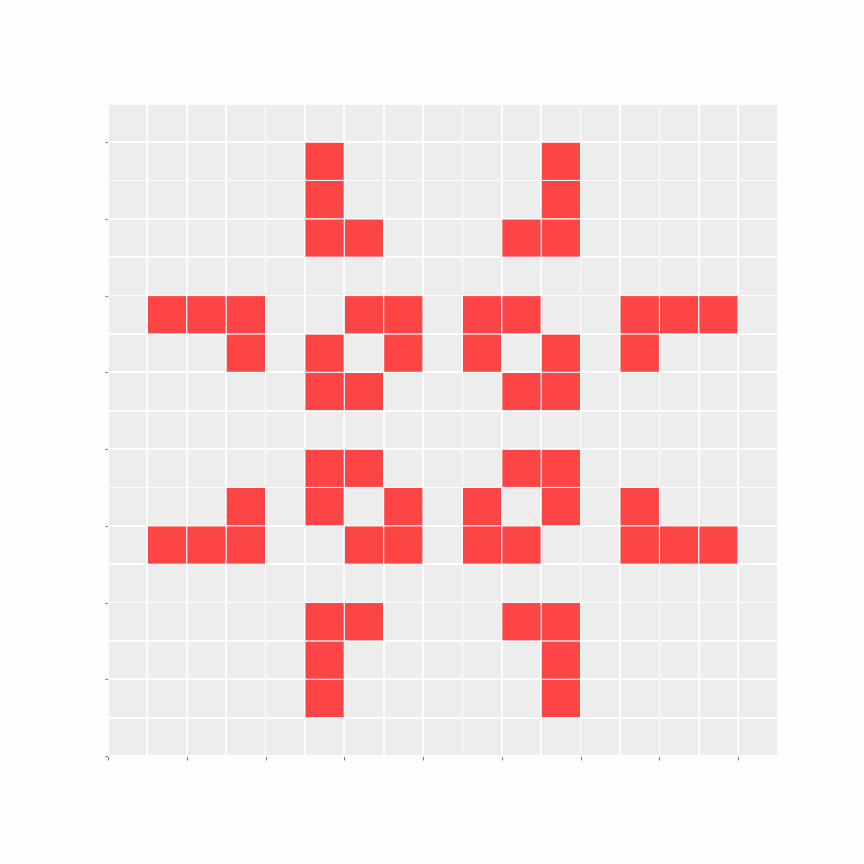
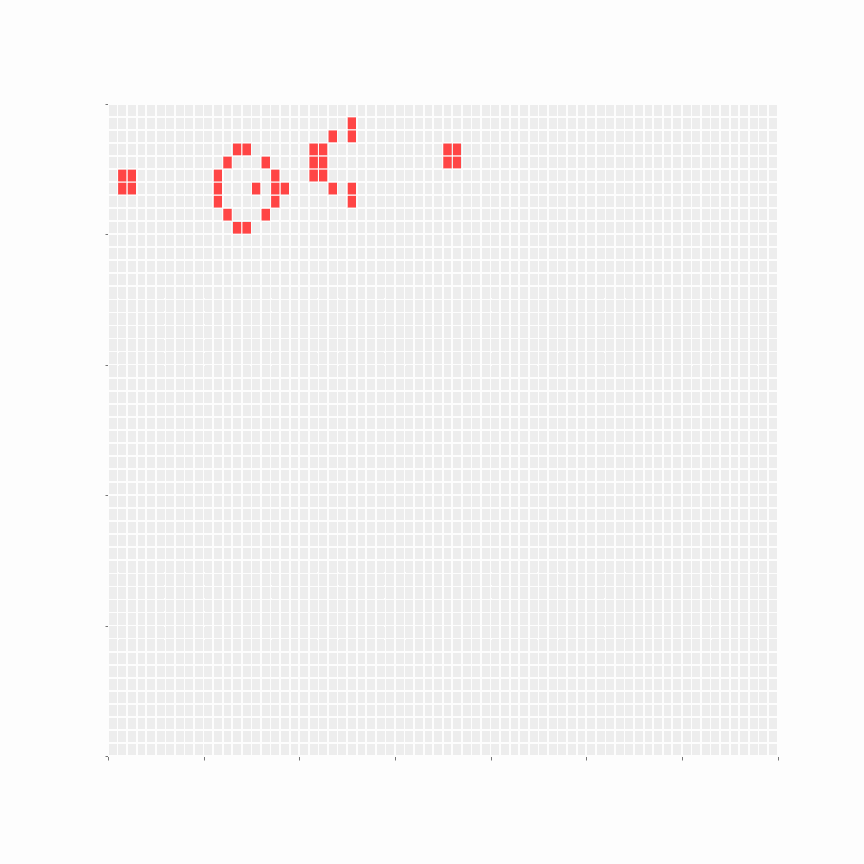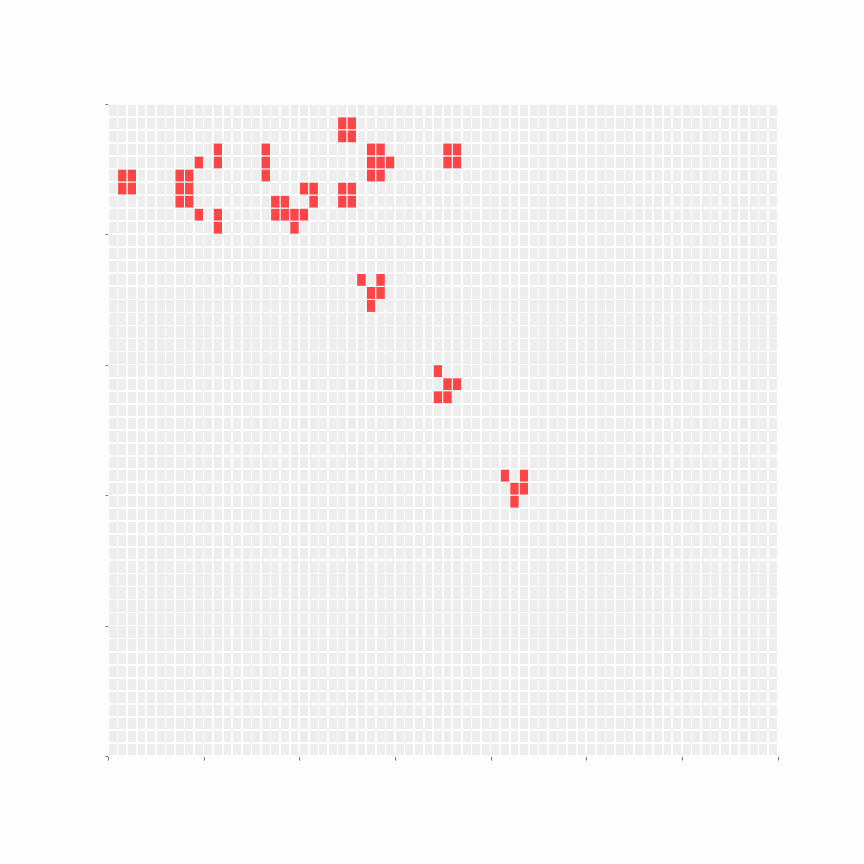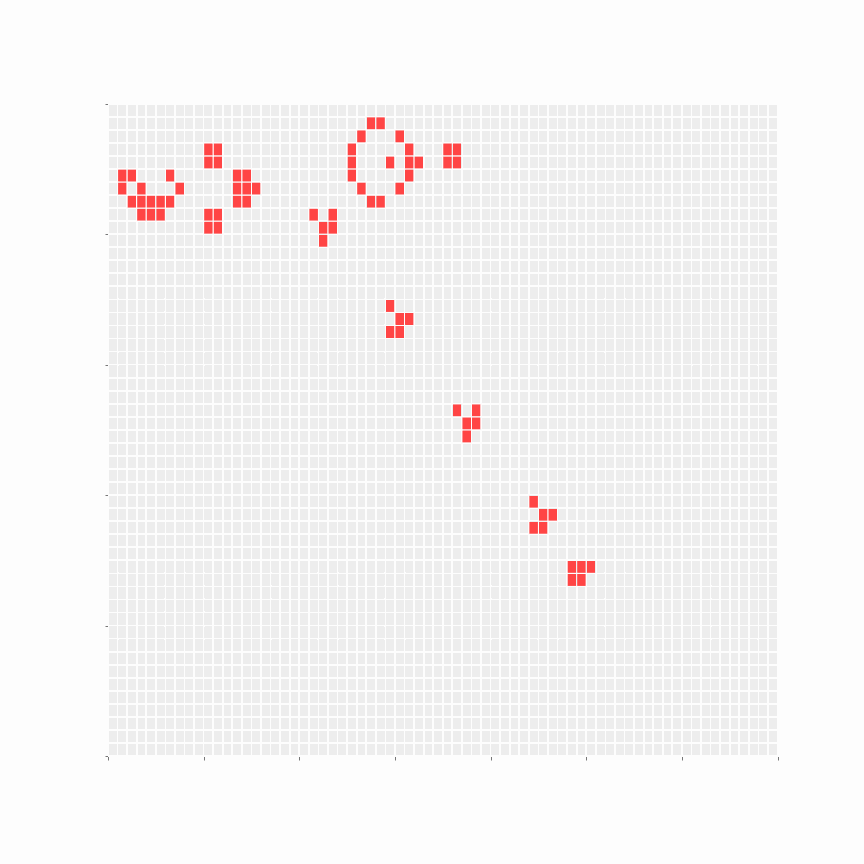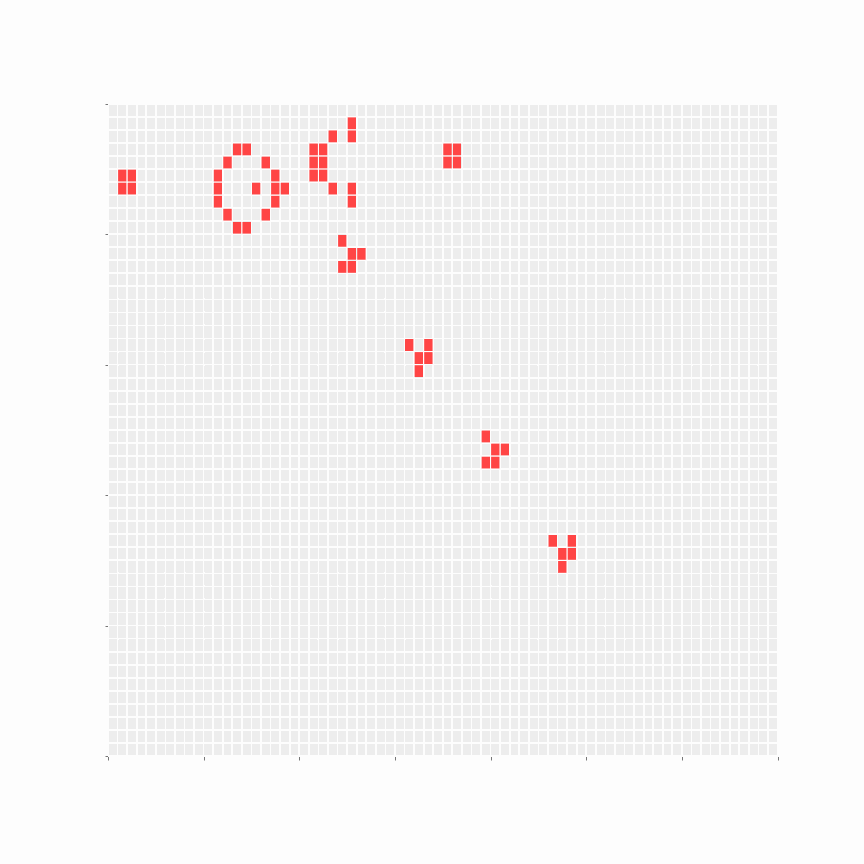
As GoL is Turing complete, it can be used to simulate a Turing machine. This paper demonstrates the same; it is fascinating.

And personal favourite — Life in Life: